Visualising Temporal Trends

Introduction

This tutorial provides good practices regarding visualisation and interpretation of trends of indicators over time. The methods discussed here are more broadly applicable, be for this tutorial we focus on occurrence cubes from which biodiversity indicators are derived. For visualisation and interpretation, we strongly rely on the functionality and concepts of the effectclass package.

Calculating confidence intervals with dubicube

We reuse the example introduced in bootstrap confidence interval calculation tutorial where we calculate confidence limits for the mean number of observations per grid cell per year for birds in Belgium between 2011 en 2020 using the MGRS grid at 10 km scale.

# Load packages
library(dubicube)

# Data loading and processing
library(frictionless) # Load example datasets
library(b3gbi)        # Process occurrence cubes

# General
library(ggplot2)      # Data visualisation
library(dplyr)        # Data wrangling
library(tidyr)        # Data wrangling

Loading and processing the data

We load the bird cube data from the b3data data package using frictionless (see also here).

# Read data package
b3data_package <- read_package(
  "https://zenodo.org/records/15211029/files/datapackage.json"
)

# Load bird cube data
bird_cube_belgium <- read_resource(b3data_package, "bird_cube_belgium_mgrs10")
head(bird_cube_belgium)
#> # A tibble: 6 × 8
#>    year mgrscode specieskey species          family     n mincoordinateuncerta…¹
#>   <dbl> <chr>         <dbl> <chr>            <chr>  <dbl>                  <dbl>
#> 1  2000 31UDS65     2473958 Perdix perdix    Phasi…     1                   3536
#> 2  2000 31UDS65     2474156 Coturnix coturn… Phasi…     1                   3536
#> 3  2000 31UDS65     2474377 Fulica atra      Ralli…     5                   1000
#> 4  2000 31UDS65     2475443 Merops apiaster  Merop…     6                   1000
#> 5  2000 31UDS65     2480242 Vanellus vanell… Chara…     1                   3536
#> 6  2000 31UDS65     2480637 Accipiter nisus  Accip…     1                   3536
#> # ℹ abbreviated name: ¹​mincoordinateuncertaintyinmeters
#> # ℹ 1 more variable: familycount <dbl>

We process the cube with b3gbi. First, we select 2000 random rows to make the dataset smaller. This is to reduce the computation time for this tutorial. We select the data from 2011 - 2020.

set.seed(123)

# Make dataset smaller
rows <- sample(nrow(bird_cube_belgium), 2000)
bird_cube_belgium <- bird_cube_belgium[rows, ]

# Process cube
processed_cube <- process_cube(
  bird_cube_belgium,
  first_year = 2011,
  last_year = 2020,
  cols_occurrences = "n"
)
processed_cube
#> 
#> Processed data cube for calculating biodiversity indicators
#> 
#> Date Range: 2011 - 2020 
#> Single-resolution cube with cell size 10km ^2 
#> Number of cells: 242 
#> Grid reference system: mgrs 
#> Coordinate range:
#>    xmin    xmax    ymin    ymax 
#>  280000  710000 5490000 5700000 
#> 
#> Total number of observations: 45143 
#> Number of species represented: 253 
#> Number of families represented: 57 
#> 
#> Kingdoms represented: Data not present 
#> 
#> First 10 rows of data (use n = to show more):
#> 
#> # A tibble: 957 × 13
#>     year cellCode taxonKey scientificName    family   obs minCoordinateUncerta…¹
#>    <dbl> <chr>       <dbl> <chr>             <chr>  <dbl>                  <dbl>
#>  1  2011 31UFS56   5231918 Cuculus canorus   Cucul…    11                   3536
#>  2  2011 31UES28   5739317 Phoenicurus phoe… Musci…     6                   3536
#>  3  2011 31UFS64   6065824 Chroicocephalus … Larid…   143                   1000
#>  4  2011 31UFS96   2492576 Muscicapa striata Musci…     3                   3536
#>  5  2011 31UES04   5231198 Passer montanus   Passe…     1                   3536
#>  6  2011 31UES85   5229493 Garrulus glandar… Corvi…    23                    707
#>  7  2011 31UES88  10124612 Anser anser x Br… Anati…     1                    100
#>  8  2011 31UES22   2481172 Larus marinus     Larid…     8                   1000
#>  9  2011 31UFS43   2481139 Larus argentatus  Larid…    10                   3536
#> 10  2011 31UFT00   9274012 Spatula querqued… Anati…     8                   3536
#> # ℹ 947 more rows
#> # ℹ abbreviated name: ¹​minCoordinateUncertaintyInMeters
#> # ℹ 6 more variables: familyCount <dbl>, xcoord <dbl>, ycoord <dbl>,
#> #   utmzone <int>, hemisphere <chr>, resolution <chr>

Analysis of the data

Let’s say we are interested in the mean number of observations per grid cell per year. We create a function to calculate this.

# Function to calculate statistic of interest
# Mean observations per grid cell per year
mean_obs <- function(data) {
  data %>%
    dplyr::mutate(x = mean(obs), .by = "cellCode") %>%
    dplyr::summarise(diversity_val = mean(x), .by = "year") %>%
    as.data.frame()
}

We get the following results:

mean_obs(processed_cube$data)
#>    year diversity_val
#> 1  2011      34.17777
#> 2  2012      35.27201
#> 3  2013      33.25581
#> 4  2014      55.44160
#> 5  2015      49.24754
#> 6  2016      48.34063
#> 7  2017      70.42202
#> 8  2018      48.83850
#> 9  2019      47.46795
#> 10 2020      43.00411

On their own, these values don’t reveal how much uncertainty surrounds them. To better understand their variability, we use bootstrapping to estimate the distribution of the yearly means. From this, we can calculate bootstrap confidence intervals.

Bootstrapping

We use the bootstrap_cube() function to perform bootstrapping (see also the bootstrap tutorial).

bootstrap_results <- bootstrap_cube(
  data_cube = processed_cube,
  fun = mean_obs,
  grouping_var = "year",
  samples = 1000,
  seed = 123
)

head(bootstrap_results)
#>   sample year est_original rep_boot est_boot se_boot  bias_boot
#> 1      1 2011     34.17777 24.23133 33.80046 4.24489 -0.3773142
#> 2      2 2011     34.17777 24.28965 33.80046 4.24489 -0.3773142
#> 3      3 2011     34.17777 31.81445 33.80046 4.24489 -0.3773142
#> 4      4 2011     34.17777 33.42530 33.80046 4.24489 -0.3773142
#> 5      5 2011     34.17777 35.03502 33.80046 4.24489 -0.3773142
#> 6      6 2011     34.17777 33.72037 33.80046 4.24489 -0.3773142

Interval calculation

Now we can use the calculate_bootstrap_ci() function to calculate confidence limits (see also the bootstrap confidence interval calculation tutorial). We get a warning message for BCa calculation because we are using a relatively small dataset.

ci_mean_obs <- calculate_bootstrap_ci(
  bootstrap_samples_df = bootstrap_results,
  grouping_var = "year",
  type = c("perc", "bca", "norm", "basic"),
  conf = 0.95,
  data_cube = processed_cube,   # Required for BCa
  fun = mean_obs                # Required for BCa
)
#> Warning in norm_inter(h(t), adj_alpha): Extreme order statistics used as
#> endpoints.
#> Warning in norm_inter(h(t), adj_alpha): Extreme order statistics used as
#> endpoints.

# Make interval type factor
ci_mean_obs <- ci_mean_obs %>%
  mutate(
    int_type = factor(
      int_type, levels = c("perc", "bca", "norm", "basic")
    )
  )

head(ci_mean_obs)
#>   year est_original est_boot   se_boot  bias_boot int_type conf       ll
#> 1 2011     34.17777 33.80046  4.244890 -0.3773142     perc 0.95 26.57582
#> 2 2012     35.27201 34.45877  3.776430 -0.8132403     perc 0.95 27.23367
#> 3 2013     33.25581 33.72937  5.351881  0.4735622     perc 0.95 24.91414
#> 4 2014     55.44160 53.13004 10.597359 -2.3115608     perc 0.95 36.04170
#> 5 2015     49.24754 48.60624  9.888400 -0.6412965     perc 0.95 34.60635
#> 6 2016     48.34063 47.10668 11.388627 -1.2339492     perc 0.95 30.82583
#>         ul
#> 1 42.77975
#> 2 41.66334
#> 3 46.62692
#> 4 77.37950
#> 5 73.13698
#> 6 73.16598

Visualising uncertainty in temporal trends

Error bars

The use of error bars is an easy and straightforward way to visualise uncertainty around indicator estimates.

ci_mean_obs %>%
  ggplot(aes(x = year, y = est_original)) +
  # Intervals
  geom_errorbar(aes(ymin = ll, ymax = ul),
                position = position_dodge(0.8), linewidth = 0.8) +
  # Estimates
  geom_point(colour = "firebrick", size = 2) +
  # Settings
  labs(y = "Mean Number of Observations\nper Grid Cell") +
  scale_x_continuous(breaks = sort(unique(bootstrap_results$year))) +
  theme_minimal() +
  facet_wrap(~int_type)

However, the question remains which interval types should be calculated and/or reported. A good idea is to compare different interval types next to each other together with the bootstrap distribution and the bootstrap bias (the difference between the estimate and the bootstrap estimate).

# Get bias vales
bias_mean_obs <- bootstrap_results %>%
  distinct(year, estimate = est_original, `bootstrap estimate` = est_boot)

# Get estimate values
estimate_mean_obs <- bias_mean_obs %>%
  pivot_longer(cols = c("estimate", "bootstrap estimate"),
               names_to = "Legend", values_to = "value") %>%
  mutate(Legend = factor(Legend, levels = c("estimate", "bootstrap estimate"),
                         ordered = TRUE))
# Visualise
bootstrap_results %>%
  ggplot(aes(x = year)) +
  # Distribution
  geom_violin(aes(y = rep_boot, group = year),
              fill = alpha("cornflowerblue", 0.2)) +
  # Estimates and bias
  geom_point(data = estimate_mean_obs, aes(y = value, shape = Legend),
             colour = "firebrick", size = 2, alpha = 0.5) +
  # Intervals
  geom_errorbar(data = ci_mean_obs,
                aes(ymin = ll, ymax = ul, colour = int_type),
                position = position_dodge(0.8), linewidth = 0.6) +
  # Settings
  labs(y = "Mean Number of Observations\nper Grid Cell",
       x = "", shape = "Legend:", colour = "Interval type:") +
  scale_x_continuous(breaks = sort(unique(bootstrap_results$year))) +
  theme_minimal() +
  theme(legend.position = "bottom",
        legend.title = element_text(face = "bold"))
#> Warning: Using shapes for an ordinal variable is not advised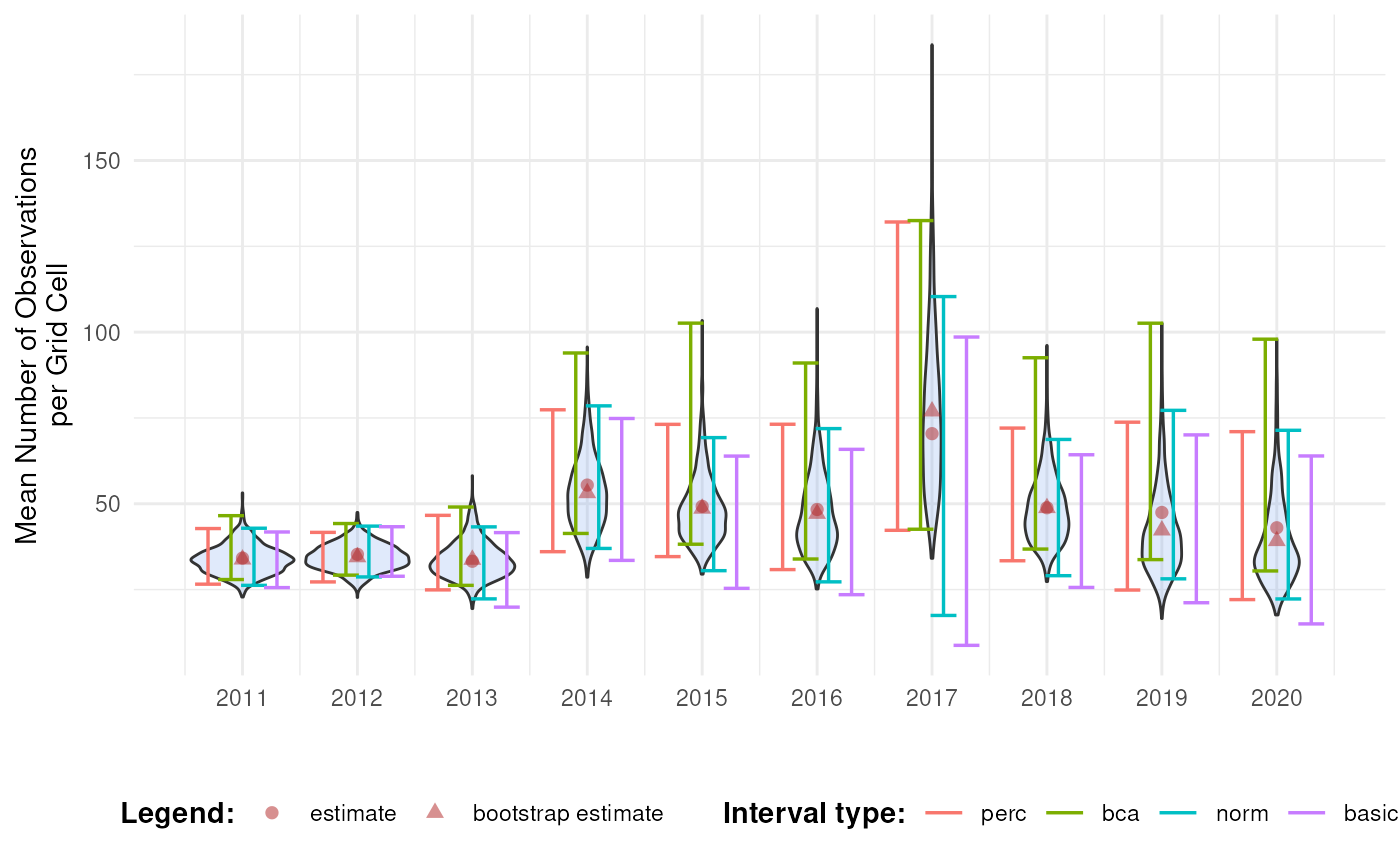

This informs us about the shape of the bootstrap distribution and the amount of bootstrap bias. In combination with bootstrap interval theory, it can be decided which interval type(s) should be reported. In general, because of the wide range of biodiversity indicator types, we recommend the use of percentile or BCa intervals, because they have no strong assumptions regarding the bootstrap distribution. The BCa interval is recommended as it accounts for bias and skewness. However, due to the jackknife estimation of the acceleration parameter, the calculation time is significantly longer. The use of the normal and basic confidence intervals is not recommended, but could be used in combination with truncations or transformations. The assumption of normality can be checked by making a Q-Q plot of the bootstrap replications (see further) (Davison & Hinkley, 1997). An overview of the recommendations is provided in the table below. This is not an exhaustive review of the topic, but based on existing literature and our preliminary results, these recommendations provide a useful starting point for selecting appropriate interval types.

Interval type	Advantages	Disadvantages	References
Normal	Simplicity Understanding of bootstrap and CI theory	Assumes bootstrap distribution is normal Often, transformation needed for more accurate results Erratic coverage error in practice	Davison & Hinkley (1997, Ch. 5); Efron & Tibshirani (1994, Ch. 13); Hesterberg (2015)
Basic	Simplicity Understanding of bootstrap and CI theory	Assumes symmetric bootstrap distribution Typically substantial coverage error	Carpenter & Bithell (2000); Davison & Hinkley (1997, Ch. 5); Hesterberg (2015)
Percentile	Simplicity No assumptions about bootstrap distribution Implicitly uses the existence of a good transformation	Does not take bias into account Substantial coverage error if the distribution is not nearly symmetric	Carpenter & Bithell (2000); Davison & Hinkley (1997, Ch. 5); Efron & Tibshirani (1994, Ch. 13)
BCa	No assumptions about bootstrap distribution Implicitly uses the existence of a good transformation Adjusts for bias Adjusts for skewness Smaller coverage error than the other methods	Involved calculation of acceleration parameter a Unstable coverage when sample size is small or a is small	Carpenter & Bithell (2000); Davison & Hinkley (1997, Ch. 5); Dixon (2000); Efron & Tibshirani (1994, Ch. 14)

Smooth trends

To create a more continuous representation of change over time, we can apply LOESS (Locally Estimated Scatterplot Smoothing) to the estimates and confidence limits. This smoothing technique fits local regressions across subsets of the data, producing a flexible trend line that helps visualize broader patterns while retaining important details.

It should be noted that this may complicate interpretation of the results. Occurrence cubes are by definition categorical over time (in this case by year), so smoothing things out over time while the data have been aggregated might lead to different results compared to a similar analysis on the original data (before the cube was made and aggregation occurred). Therefore, we recommend this visualisation for long time series to make general interpretations of the trend over time. In our example, we actually have a small time frame so we only show this for the sake of the tutorial.

Based on the discussion above, we select the BCa interval as we see some asymmetry and bias in the bootstrap distribution of later years. Note that this is probably due to the selection 2000 random rows from the original dataset to reduce the computation time for this tutorial. Otherwise we would expect a more symmetrical distribution for this indicator.

ci_mean_obs %>%
  filter(int_type == "bca") %>%
  ggplot(aes(x = year, y = est_original)) +
  geom_smooth(
    colour = alpha("blue", 0.5),
    linetype = "solid",
    method = "loess",
    formula = "y ~ x",
    se = FALSE
  ) +
  geom_smooth(
    aes(y = ul),
    colour = alpha("lightsteelblue1", 1),
    linetype = "dashed",
    method = "loess",
    formula = "y ~ x",
    se = FALSE
  ) +
  geom_smooth(
    aes(y = ll),
    colour = alpha("lightsteelblue1", 1),
    linetype = "dashed",
    method = "loess",
    formula = "y ~ x",
    se = FALSE
  ) +
  geom_ribbon(
    aes(ymin = predict(loess(ll ~ year)), ymax = predict(loess(ul ~ year))),
    alpha = 0.2, fill = "lightsteelblue1"
  ) +
  # Intervals
  geom_errorbar(aes(ymin = ll, ymax = ul),
                position = position_dodge(0.8), linewidth = 0.8) +
  # Estimates
  geom_point(colour = "firebrick", size = 3) +
  # Settings
  labs(y = "Mean Number of Observations\nper Grid Cell") +
  scale_x_continuous(breaks = sort(unique(bootstrap_results$year))) +
  theme_minimal()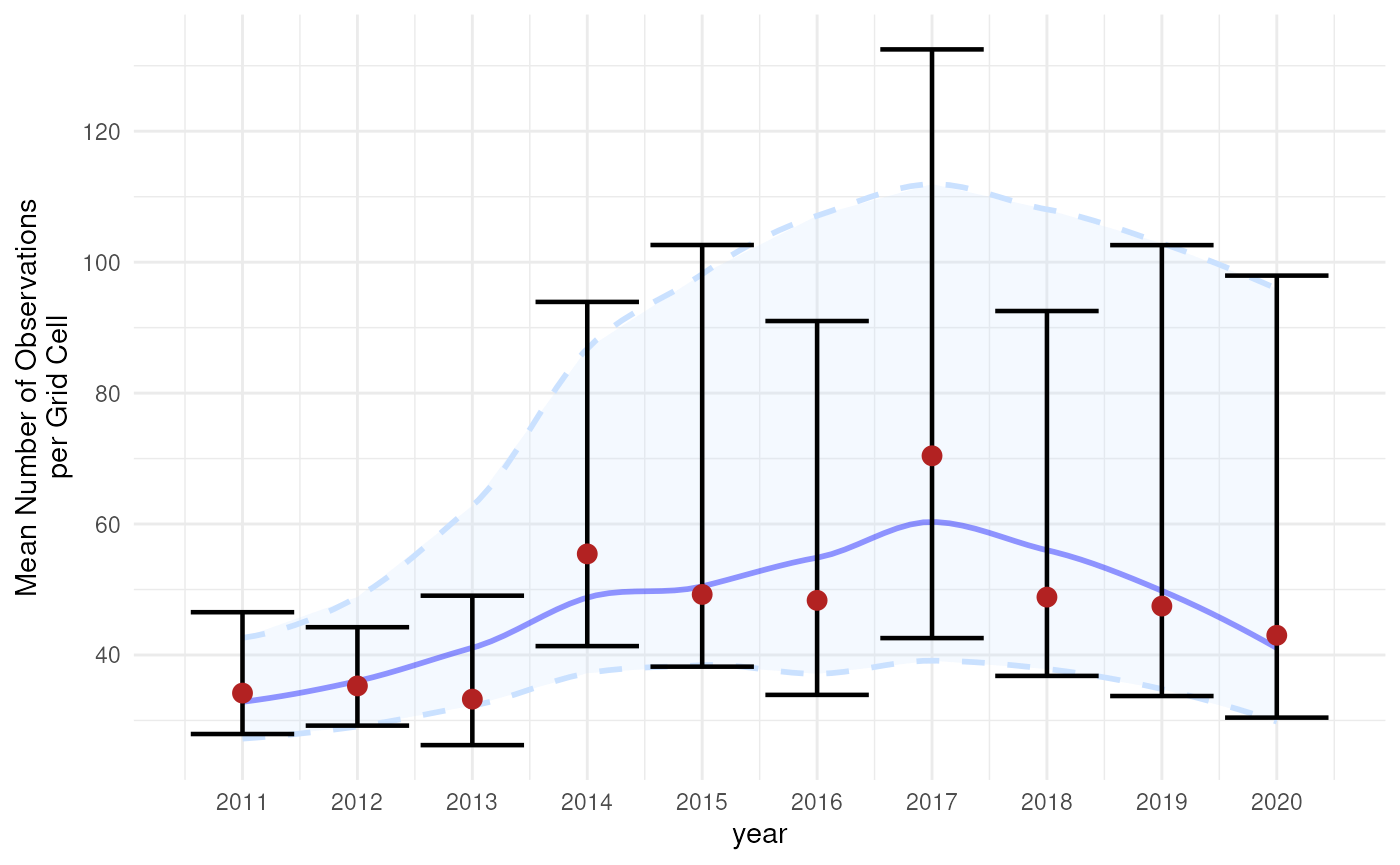

Fan plots

The effectclass package provides the stat_fan() function to create fan plot intervals (see also this effectclass tutorial).

library(effectclass)

These intervals are based on a normal distribution or a transformation via the link argument. Therefore, we check the assumption of normality by making a Q-Q plot of the bootstrap replications.

ggplot(bootstrap_results, aes(sample = rep_boot)) +
  # Q-Q plot
  stat_qq() +
  stat_qq_line(col = "red") +
  # Settings
  labs(x = "Theoretical Quantiles (Standard Normal)",
       y = "Sample Quantiles (Bootstrap Replicates)") +
  facet_wrap(~ year, ncol = 2, scales = "free") +
  theme_minimal()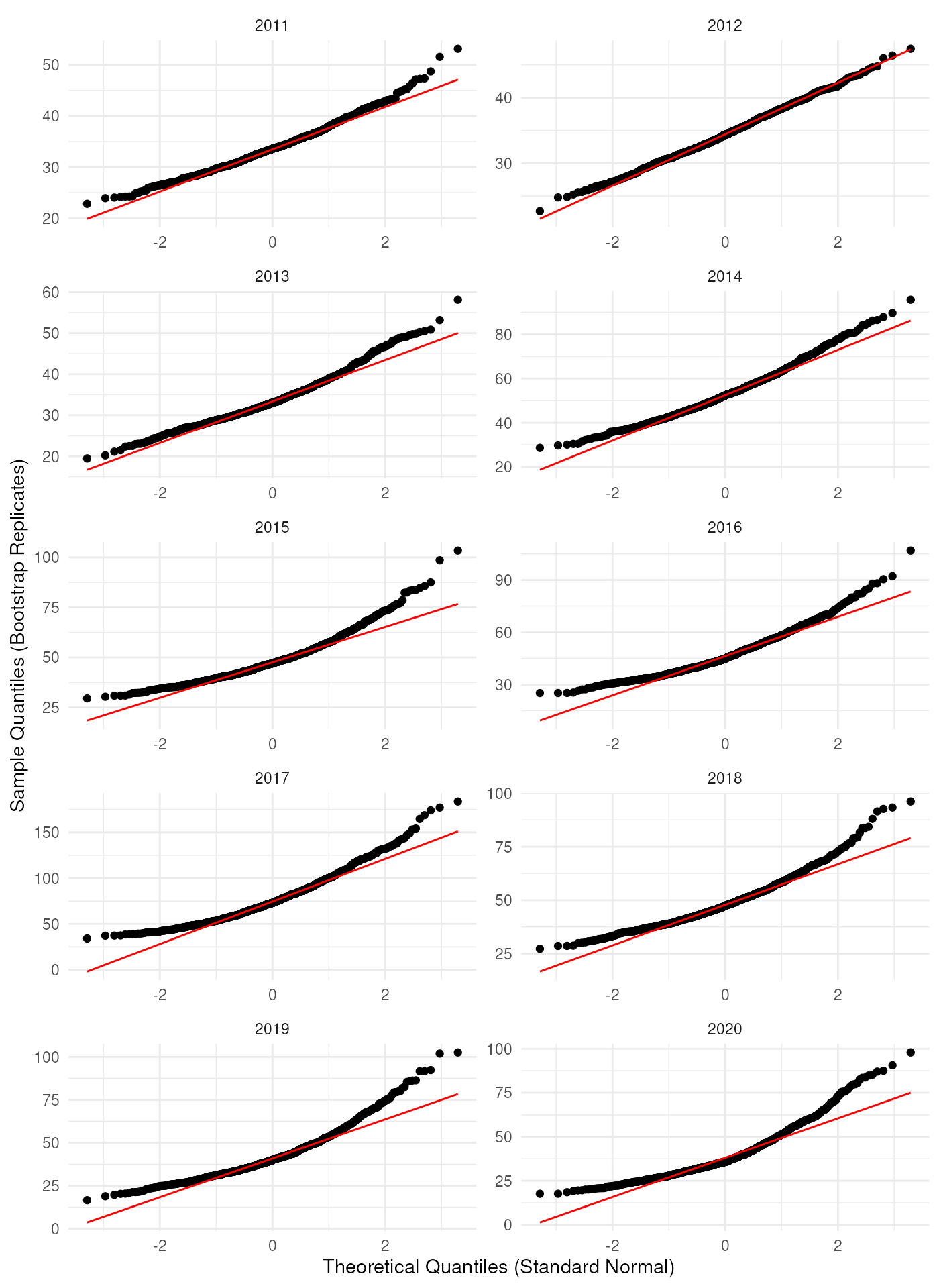

As expected, it looks like the bootstrap distributions are not normally distributed in most years. If we log-transform the bootstrap replications, the Q-Q plots look better.

ggplot(bootstrap_results, aes(sample = log(rep_boot))) +
  # Q-Q plot
  stat_qq() +
  stat_qq_line(col = "red") +
  # Settings
  labs(x = "Theoretical Quantiles (Standard Normal)",
       y = "Sample Quantiles (Bootstrap Replicates)") +
  facet_wrap(~ year, ncol = 2, scales = "free") +
  theme_minimal()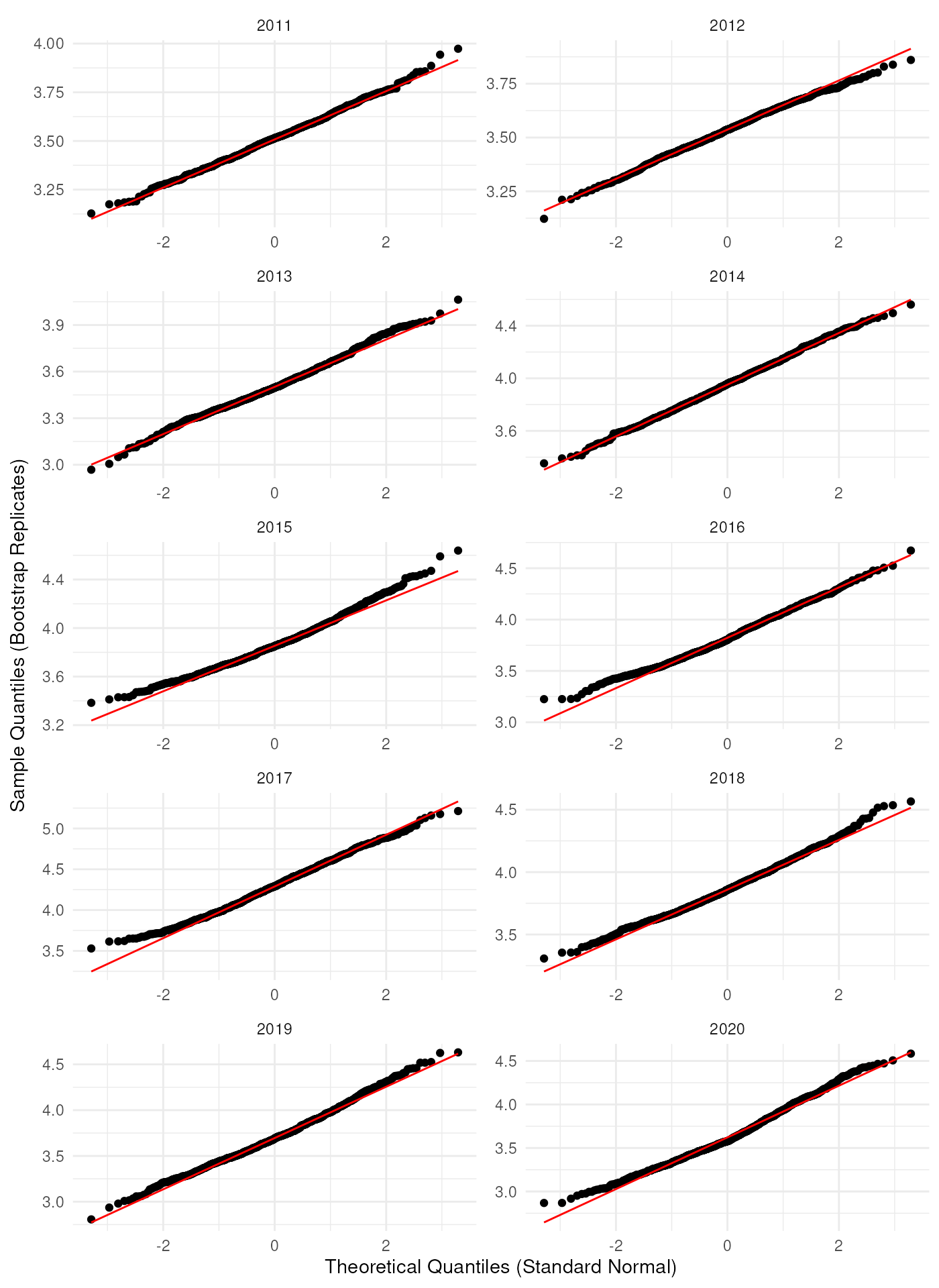

We therefore calculate the log-transformed normal intervals and compare them with the BCa and normal intervals.

ci_mean_obs_lognorm <- calculate_bootstrap_ci(
  bootstrap_samples_df = bootstrap_results,
  grouping_var = "year",
  type = c("norm"),
  conf = 0.95,
  h = log,
  hinv = exp
)

The log-normal intervals look indeed more correct then the normal intervals, although they still differ from the BCa intervals.

# Combine interval data
ci_mean_obs_new <- ci_mean_obs %>%
  filter(int_type %in% c("bca", "norm")) %>%
  bind_rows(ci_mean_obs_lognorm %>% mutate(int_type = "log_norm"))

# Visualise
bootstrap_results %>%
  ggplot(aes(x = year)) +
  # Distribution
  geom_violin(aes(y = rep_boot, group = year),
              fill = alpha("cornflowerblue", 0.2)) +
  # Estimates and bias
  geom_point(data = estimate_mean_obs, aes(y = value, shape = Legend),
             colour = "firebrick", size = 2, alpha = 0.5) +
  # Intervals
  geom_errorbar(data = ci_mean_obs_new,
                aes(ymin = ll, ymax = ul, colour = int_type),
                position = position_dodge(0.8), linewidth = 0.6) +
  # Settings
  labs(y = "Mean Number of Observations\nper Grid Cell",
       x = "", shape = "Legend:", colour = "Interval type:") +
  scale_x_continuous(breaks = sort(unique(bootstrap_results$year))) +
  theme_minimal() +
  theme(legend.position = "bottom",
        legend.title = element_text(face = "bold"))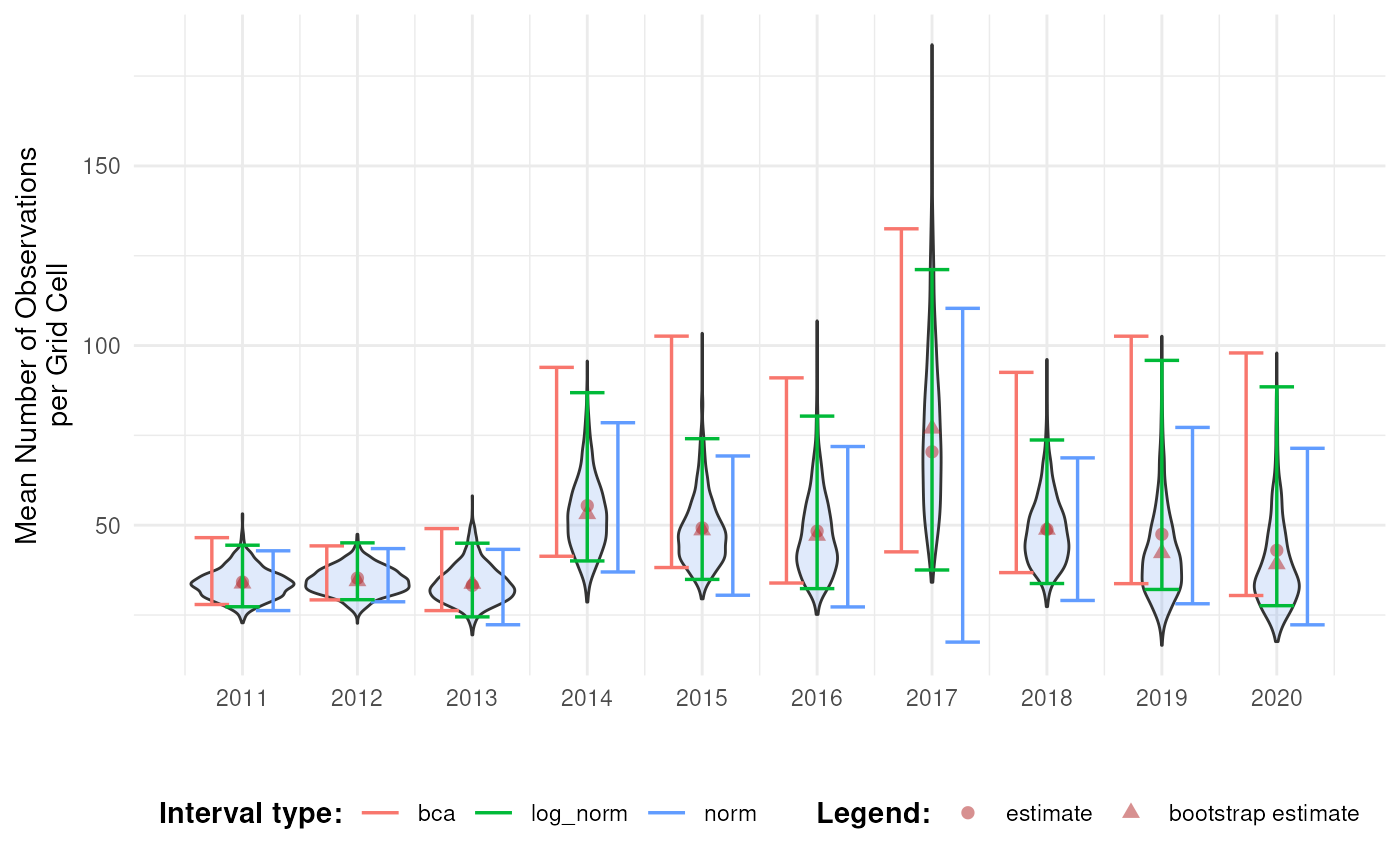

Finally, we can create a fan plot assuming the log-normal distribution. Note that for stat_fan(), the link_sd is the standard error on the link scale, while y is on the natural scale. So we have to recalculate the standard error on the log-transformed bootstrap replicates. We also need to account for bias. As noted in the previous section, year is a discrete variable in our data cube. We therefore use the geom = "rect" option.

bootstrap_results %>%
  # Calculate standard error on link scale
  mutate(rep_boot_log = log(rep_boot),
         est_boot_log = mean(rep_boot_log), # Needed for bias calculation
         se_boot_log = sd(rep_boot_log),
         .by = "year") %>%
  # Get unique estimates per year
  distinct(year, est_original, est_boot_log, se_boot_log) %>%
  # Calculate bias factor
  mutate(bias_log = exp(est_boot_log - log(est_original))) %>%
  # Visualise
  ggplot(aes(x = year)) +
  effectclass::stat_fan(
    aes(y = est_original / bias_log, link_sd = se_boot_log),
    link = "log", fill = "cornflowerblue", max_prob = 0.95,
    geom = "rect"
  ) +
  # Settings
  labs(y = "Mean Number of Observations\nper Grid Cell", x = "") +
  scale_x_continuous(breaks = sort(unique(bootstrap_results$year))) +
  theme_minimal()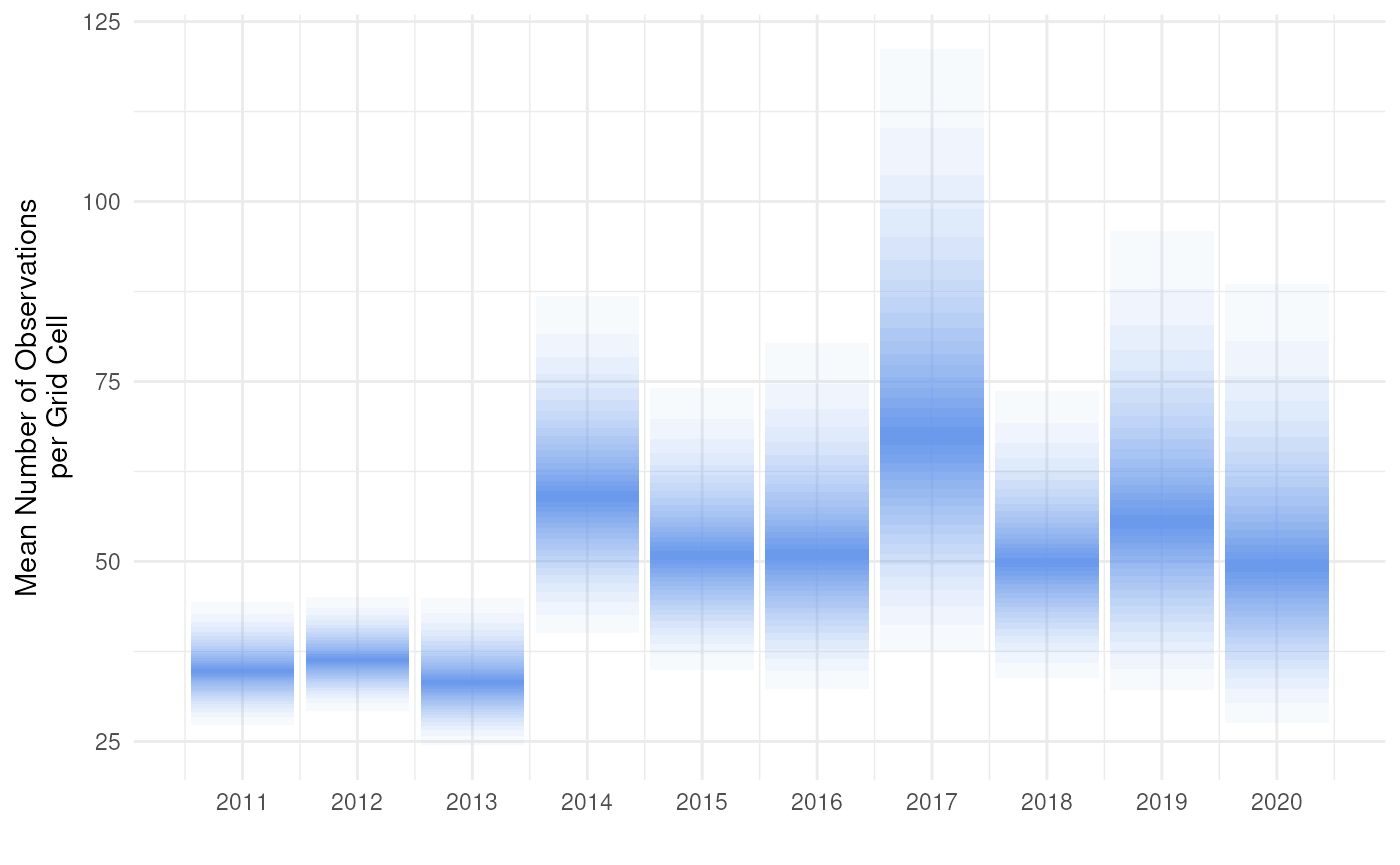

We can make use of this concept to make fan plots for other interval types ourselves. We calculate BCA and log-normal intervals for five coverages using a for loop.

# Set up coverage levels
max_prob <- 0.95
step <- 0.2
coverages <- seq(max_prob, 1e-3, by = -step)

# Loop over coverages
out_ci_list <- vector(mode = "list", length = length(coverages))

for (i in seq_along(coverages)) {
  cov <- coverages[i]

  # Calculate confidence limits for confidence level
  ci_cov <- calculate_bootstrap_ci(
    bootstrap_samples_df = bootstrap_results,
    grouping_var = "year",
    type = c("bca", "norm"),
    conf = cov,
    h = log,
    hinv = exp,
    data_cube = processed_cube,   # Required for BCa
    fun = mean_obs                # Required for BCa
  )

  out_ci_list[[i]] <- ci_cov
}
out_ci <- bind_rows(out_ci_list) %>%
  mutate(int_type = ifelse(int_type == "norm", "log_norm", int_type))

We can visualise this in a categorical way with geom_rect() from ggplot2.

# For visualisation of envelopes
alpha_levels <- sapply(coverages, function(i) 1 - i / (i + step))
names(alpha_levels) <- as.character(coverages)

# Convert conf to character so it can match alpha_levels
out_ci <- out_ci %>%
  mutate(
    conf_chr = as.character(conf),
    year_num = as.numeric(as.factor(year)) # Numeric year for xmin/xmax
  )

# Visualise
bar_width <- 0.9

ggplot(out_ci, aes()) +
  geom_rect(
    aes(
      xmin = year_num - bar_width / 2,
      xmax = year_num + bar_width / 2,
      ymin = ll,
      ymax = ul,
      fill = conf_chr,
      alpha = conf_chr
    )
  ) +
  # Colour ribbons
  scale_alpha_manual(values = alpha_levels, name = "conf") +
  scale_fill_manual(values = rep("cornflowerblue", length(alpha_levels)),
                    name = "conf") +
  # Settings
  labs(y = "Mean Number of Observations\nper Grid Cell", x = "") +
  scale_x_continuous(
    breaks = unique(out_ci$year_num),
    labels = unique(out_ci$year)
  ) +
  facet_wrap(~int_type, ncol = 1) +
  theme_minimal()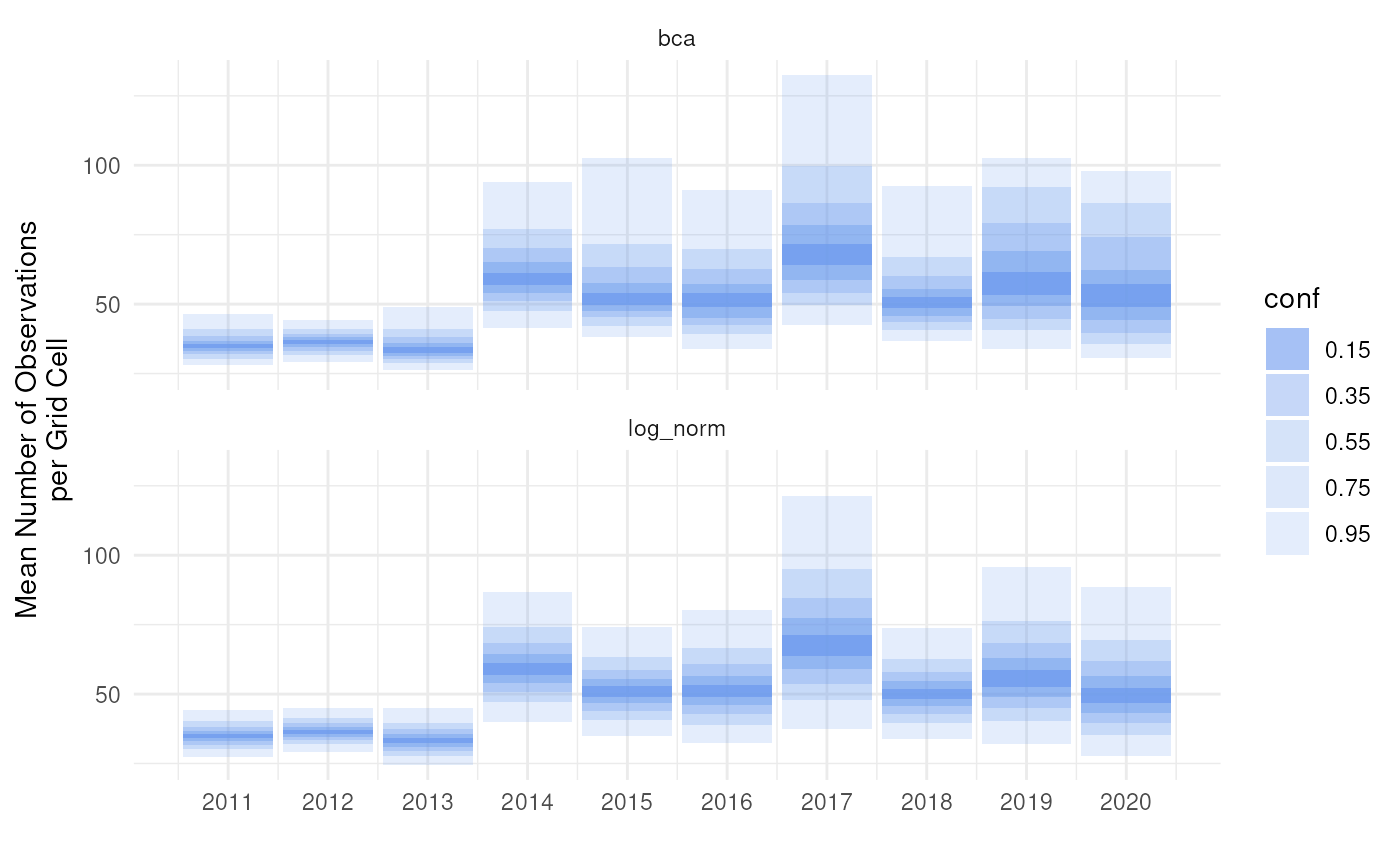

We can visualise this in a continuous way with geom_ribbon() from ggplot2. Linear (like the default of stat_fan()):

ggplot(out_ci, aes(x = year)) +
  geom_ribbon(aes(ymin = ll, ymax = ul, fill = conf_chr, alpha = conf_chr)) +
  # Colour ribbons
  scale_alpha_manual(values = alpha_levels, name = "conf") +
  scale_fill_manual(values = rep("cornflowerblue", length(alpha_levels)),
                    name = "conf") +
  # Settings
  labs(y = "Mean Number of Observations\nper Grid Cell", x = "") +
  scale_x_continuous(breaks = sort(unique(bootstrap_results$year))) +
  facet_wrap(~int_type, ncol = 1) +
  theme_minimal()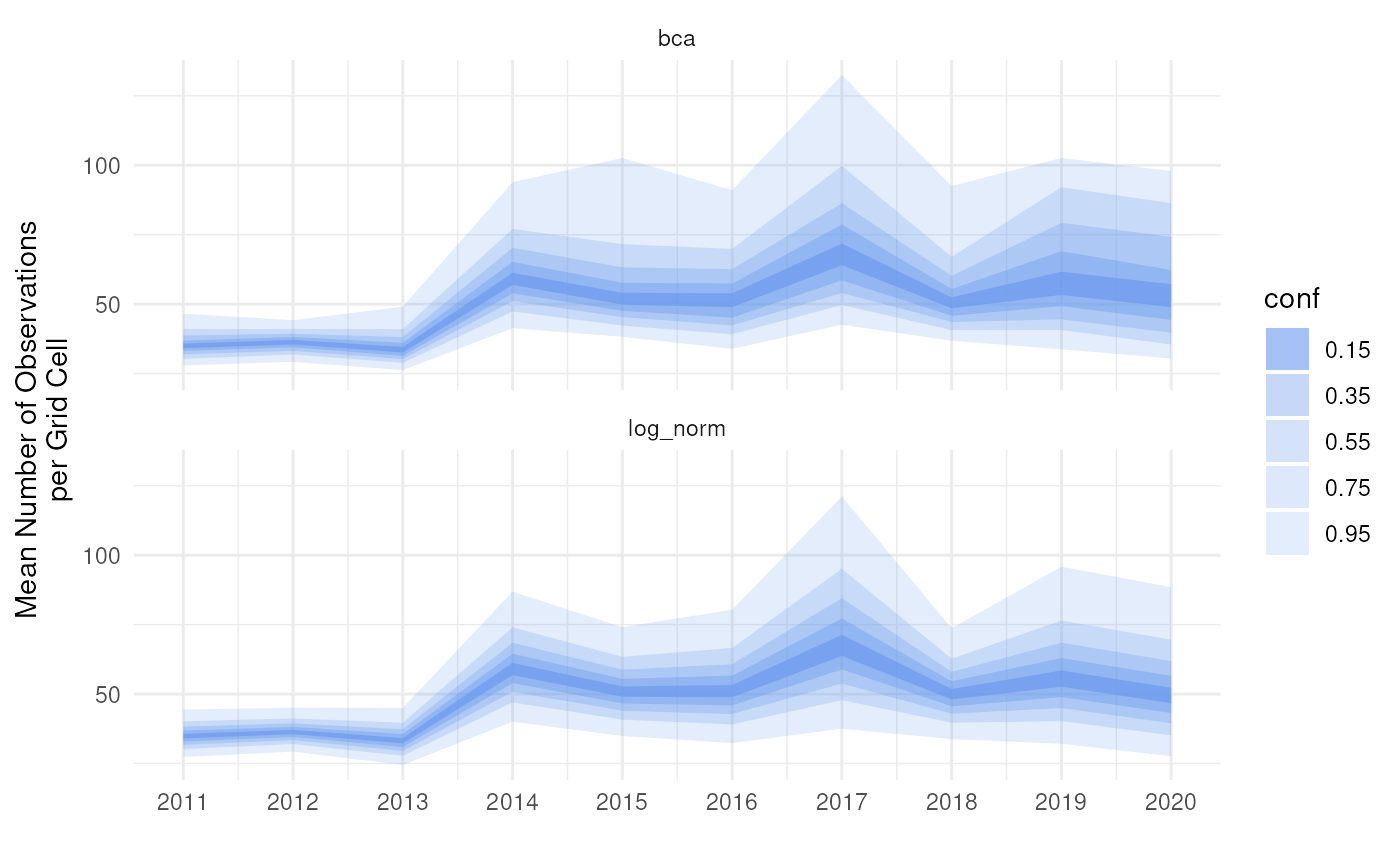

Smooth (like in the previous paragraph):

# Predict smooth ymin/ymax
out_ci %>%
  group_by(conf_chr, int_type) %>%
  mutate(ymin = predict(loess(ll ~ year)),
         ymax = predict(loess(ul ~ year))) %>%
  ungroup() %>%
  # Visualise
  ggplot(aes(x = year)) +
  geom_ribbon(
    aes(ymin = ymin, ymax = ymax, fill = conf_chr, alpha = conf_chr)
  ) +
  # Colour ribbons
  scale_alpha_manual(values = alpha_levels, name = "conf") +
  scale_fill_manual(values = rep("cornflowerblue", length(alpha_levels)),
                    name = "conf") +
  # Settings
  labs(y = "Mean Number of Observations\nper Grid Cell", x = "") +
  scale_x_continuous(breaks = sort(unique(bootstrap_results$year))) +
  facet_wrap(~int_type, ncol = 1) +
  theme_minimal()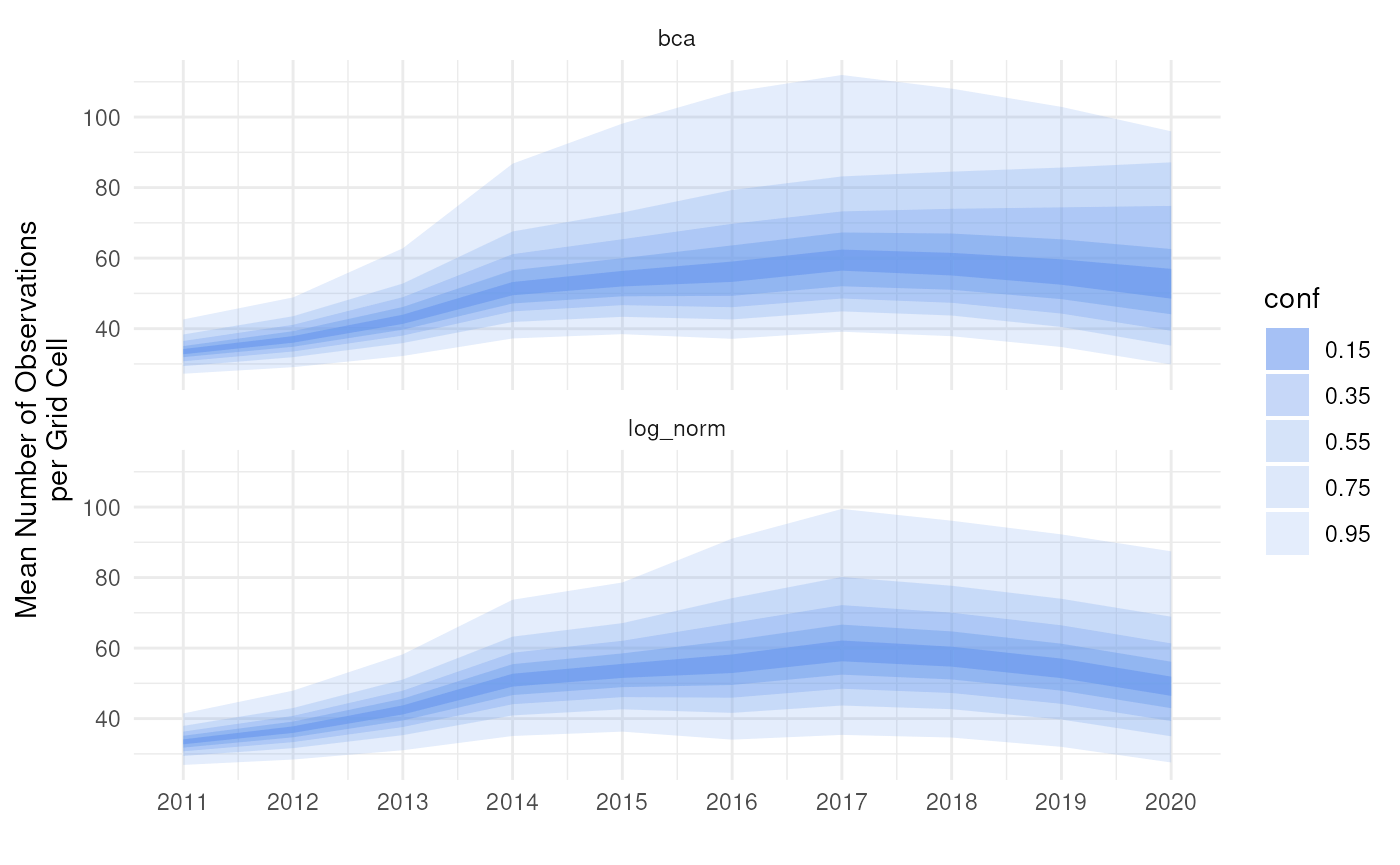

Visualising temporal effects

In this tutorial, we demonstrated how to classify effect sizes based on confidence intervals. Here we give some visualisation options based on the effectclass package (see also this effectclass tutorial).

Let’s calculate the BCa interval for the mean number of observations per grid cell compared to 2011 and perform effect classification with threshold 5.

# Bootstrapping
bootstrap_results_ref <- bootstrap_cube(
  data_cube = processed_cube,
  fun = mean_obs,
  grouping_var = "year",
  samples = 1000,
  ref_group = 2011,
  seed = 123
)

# Calculate confidence intervals
ci_mean_obs_ref <- calculate_bootstrap_ci(
  bootstrap_samples_df = bootstrap_results_ref,
  grouping_var = "year",
  type = "bca",
  data_cube = processed_cube,   # Required for BCa
  fun = mean_obs,               # Required for BCa
  ref_group = 2011              # Required for BCa
)
#> Warning in norm_inter(h(t), adj_alpha): Extreme order statistics used as
#> endpoints.
#> Warning in norm_inter(h(t), adj_alpha): Extreme order statistics used as
#> endpoints.

# Perform effect classification
result <- add_effect_classification(
  df = ci_mean_obs_ref,
  cl_columns = c("ll", "ul"),
  threshold = 5,
  reference = 0
)

# View the result
result
#>   year est_original    est_boot   se_boot  bias_boot int_type conf          ll
#> 1 2012    1.0942452  0.65831911  5.475053 -0.4359261      bca 0.95 -10.7621638
#> 2 2013   -0.9219589 -0.07108256  6.690590  0.8508764      bca 0.95 -12.8513851
#> 3 2014   21.2638321 19.32958556 10.982093 -1.9342466      bca 0.95   5.8187198
#> 4 2015   15.0697689 14.80578656 10.723767 -0.2639823      bca 0.95   2.5039329
#> 5 2016   14.1628569 13.30622198 12.131657 -0.8566350      bca 0.95  -1.7552656
#> 6 2017   36.2442462 43.13141123 23.943155  6.8871650      bca 0.95   7.1906529
#> 7 2018   14.6607335 14.98367972 10.715491  0.3229462      bca 0.95   0.3961534
#> 8 2019   13.2901788  8.46222485 13.048145 -4.8279539      bca 0.95  -0.5622564
#> 9 2020    8.8263369  5.37019562 13.084703 -3.4561413      bca 0.95  -5.3273172
#>         ul effect_code effect_code_coarse             effect effect_coarse
#> 1 11.04344           ?                  ?            unknown       unknown
#> 2 13.06589           ?                  ?            unknown       unknown
#> 3 57.17064          ++                  +    strong increase      increase
#> 4 58.08685           +                  +           increase      increase
#> 5 52.49345          ?+                  ? potential increase       unknown
#> 6 96.55713          ++                  +    strong increase      increase
#> 7 48.95507           +                  +           increase      increase
#> 8 69.67581          ?+                  ? potential increase       unknown
#> 9 65.47783           ?                  ?            unknown       unknown

The effectclass package provides the stat_effect() function that visualises the effects with colours and symbols.

ggplot(data = result, aes(x = year, y = est_original, ymin = ll, ymax = ul)) +
  effectclass::stat_effect(reference = 0, threshold = 5) +
  # Settings
  labs(y = "Mean Number of Observations\nper Grid Cell Compared to 2011",
       x = "") +
  scale_x_continuous(breaks = sort(unique(result$year))) +
  theme_minimal()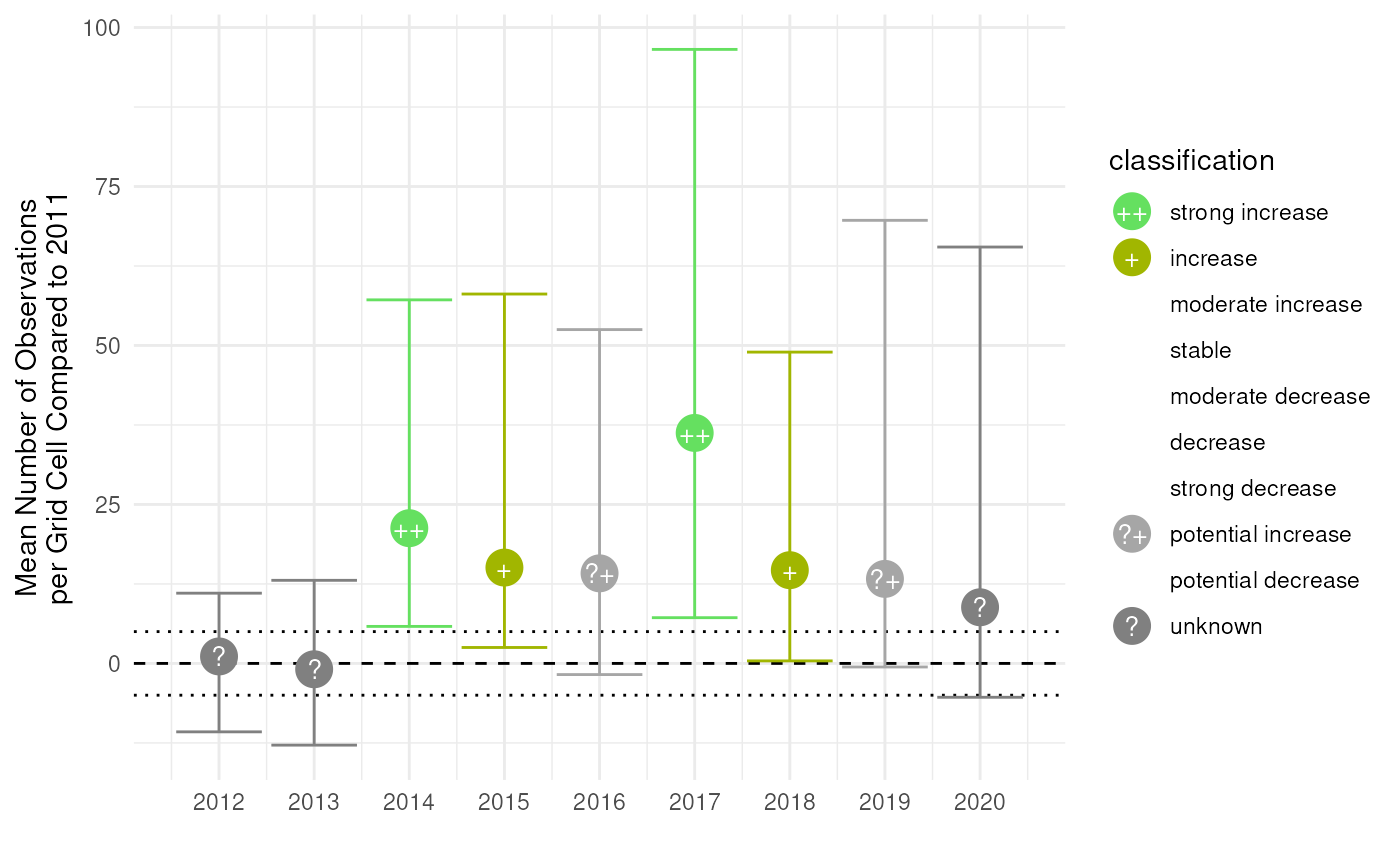

With this function, you can also add symbols to stat_fan().

Note that the choice of the reference year should be well considered. Keep in mind which comparisons should be made, and what the motivation is behind the reference period. A high or low value in the reference period relative to other periods, e.g. an exceptional bad or good year, can affect the magnitude and direction of the calculated differences. Whether this should be avoided or not, depends on the motivation behind the choice and the research question. A reference period can be determined by legislation, or by the start of a monitoring campaign. A specific research question can determine the periods that need to be compared. Furthermore, the variability of the estimate of reference period affects the width of confidence intervals for the differences. A more variable reference period will propagate greater uncertainty. In the case of GBIF data, more data will be available in recent years than in earlier years. If this is the case, it could make sense to select the last period as a reference period. In a way, this also avoids the arbitrariness of choice for the reference period. You compare previous situations with the current situation (last year), where you could repeat this comparison annually, for example. Finally, when comparing multiple indicators, we recommend using a consistent reference period to maintain comparability

References

Carpenter, J., & Bithell, J. (2000). Bootstrap confidence intervals: When, which, what? A practical guide for medical statisticians. Statistics in Medicine, 19(9), 1141–1164. https://doi.org/10.1002/(SICI)1097-0258(20000515)19:9<1141::AID-SIM479>3.0.CO;2-F

Davison, A. C., & Hinkley, D. V. (1997). Bootstrap Methods and their Application (1st ed.). Cambridge University Press. https://doi.org/10.1017/CBO9780511802843

Dixon, P. M. (2001). The Bootstrap and the Jackknife: Describing the Precision of Ecological Indices. In S. M. Scheiner & J. Gurevitch (Eds.), Design and Analysis of Ecological Experiments (Second Edition, pp. 267–288). Oxford University PressNew York, NY. https://doi.org/10.1093/oso/9780195131871.003.0014

Efron, B., & Tibshirani, R. J. (1994). An Introduction to the Bootstrap (1st ed.). Chapman and Hall/CRC. https://doi.org/10.1201/9780429246593

Hesterberg, T. C. (2015). What Teachers Should Know About the Bootstrap: Resampling in the Undergraduate Statistics Curriculum. The American Statistician, 69(4), 371–386. https://doi.org/10.1080/00031305.2015.1089789