Classifying Effects Using Confidence Limits • dubicube

Introduction

This tutorial demonstrates how to use the add_effect_classification() function to classify effect sizes based on confidence intervals. This is useful when you want to interpret uncertainty in trends or treatment effects using a transparent and rule-based approach.

About effect classification

The add_effect_classification() function takes a dataframe with confidence limits and adds classification columns that describe:

the direction and strength of the effect (e.g., strong increase, moderate decrease, unknown)
both fine-grained and coarse interpretations.

It uses the effectclass package internally to perform the classification logic. Classification is based on:

the lower and upper confidence limits around an effect estimate
a reference value (e.g., 0 for no effect)
and a threshold or range of thresholds that define what counts as a meaningful effect

Thresholds and reference values should reflect scientifically or practically meaningful changes — e.g., a biologically relevant increase or decline in a biodiversity indicator.

See the effectclass tutorial for a more elaborate overview.

Symbol	Fine effect / trend	Coarse effect / trend	Rule
`++`	strong positive effect / strong increase	positive effect / increase	confidence interval above the upper threshold
`+`	positive effect / increase	positive effect / increase	confidence interval above reference and contains the upper threshold
`+~`	moderate positive effect / moderate increase	positive effect / increase	confidence interval between reference and the upper threshold
`~`	no effect / stable	no effect / stable	confidence interval between thresholds and contains reference
`-~`	moderate negative effect / moderate decrease	negative effect / decrease	confidence interval between reference and the lower threshold
`-`	negative effect / decrease	negative effect / decrease	confidence interval below reference and contains the lower threshold
`–`	strong negative effect / strong decrease	negative effect / decrease	confidence interval below the lower threshold
`?+`	potential positive effect / potential increase	unknown effect / unknown	confidence interval contains reference and the upper threshold
`?-`	potential negative effect / potential decrease	unknown effect / unknown	confidence interval contains reference and the lower threshold
`?`	unknown effect / unknown	unknown effect / unknown	confidence interval contains the lower and upper threshold

Getting started with dubicube

# Load packages
library(dubicube)

# General
library(ggplot2)      # Data visualisation

Your dataframe must contain lower and upper confidence limits, e.g. "lcl" and "ucl". Let’s start with a synthetic dataset of 10 observations.

# Simulated means and standard deviations
ds <- data.frame(
  mean = c(0, 0.5, -0.5, 1, -1, 1.5, -1.5, 0.5, -0.5, 0),
  sd = c(1, 0.5, 0.5, 0.5, 0.5, 0.25, 0.25, 0.25, 0.25, 0.5)
)

# Compute 90% confidence intervals
ds$lcl <- qnorm(0.05, ds$mean, ds$sd)
ds$ucl <- qnorm(0.95, ds$mean, ds$sd)

# View the dataset
ds
#>    mean   sd         lcl         ucl
#> 1   0.0 1.00 -1.64485363  1.64485363
#> 2   0.5 0.50 -0.32242681  1.32242681
#> 3  -0.5 0.50 -1.32242681  0.32242681
#> 4   1.0 0.50  0.17757319  1.82242681
#> 5  -1.0 0.50 -1.82242681 -0.17757319
#> 6   1.5 0.25  1.08878659  1.91121341
#> 7  -1.5 0.25 -1.91121341 -1.08878659
#> 8   0.5 0.25  0.08878659  0.91121341
#> 9  -0.5 0.25 -0.91121341 -0.08878659
#> 10  0.0 0.50 -0.82242681  0.82242681

Add effect classifications

We use the add_effect_classification() for effect classification. It relies on the following arguments:

df: The input data, a dataframe containing confidence limits, e.g. the result of bootstrap confidence interval calculation.
cl_columns: A character vector of length 2 specifying the column names in df that contain the lower and upper confidence limits. For example: cl_columns = c("lcl", "ucl").
threshold: A numeric vector defining the effect size threshold(s) used to distinguish between “no effect” and meaningful increases or decreases. This can be either one number (interpreted symmetrically around the reference) or two (explicit lower and upper thresholds).
reference: A single numeric value representing the null hypothesis or no-effect level (e.g. 0). The position of the confidence interval relative to this value determines the direction of the effect.
coarse: A logical flag indicating whether a simplified classification should also be added. If TRUE (default), additional columns effect_code_coarse and effect_coarse are included, summarizing effects into broader categories (increase, decrease, stable, unknown).

Let’s classify the effects using a threshold of 1 (will be expanded to [-1, 1] around the reference) and a reference of 0.

# Perform effect classification
result <- add_effect_classification(
  df = ds,
  cl_columns = c("lcl", "ucl"),
  threshold = 1,
  reference = 0,
  coarse = TRUE
)

# View the result
result
#>    mean   sd         lcl         ucl effect_code effect_code_coarse
#> 1   0.0 1.00 -1.64485363  1.64485363           ?                  ?
#> 2   0.5 0.50 -0.32242681  1.32242681          ?+                  ?
#> 3  -0.5 0.50 -1.32242681  0.32242681          ?-                  ?
#> 4   1.0 0.50  0.17757319  1.82242681           +                  +
#> 5  -1.0 0.50 -1.82242681 -0.17757319           -                  -
#> 6   1.5 0.25  1.08878659  1.91121341          ++                  +
#> 7  -1.5 0.25 -1.91121341 -1.08878659          --                  -
#> 8   0.5 0.25  0.08878659  0.91121341          +~                  +
#> 9  -0.5 0.25 -0.91121341 -0.08878659          -~                  -
#> 10  0.0 0.50 -0.82242681  0.82242681           ~                  ~
#>                effect effect_coarse
#> 1             unknown       unknown
#> 2  potential increase       unknown
#> 3  potential decrease       unknown
#> 4            increase      increase
#> 5            decrease      decrease
#> 6     strong increase      increase
#> 7     strong decrease      decrease
#> 8   moderate increase      increase
#> 9   moderate decrease      decrease
#> 10             stable        stable

Visualising the result

Detailed guidance on best practices for visualising effect classifications is provided in the tutorials for temporal trends and spatial trends. Below, we demonstrate a simple and direct way to visualise classified effects using ggplot2.

# Define coarse colour palette
coarse_colour <- scale_colour_manual(
  values =  c(
    "chartreuse3",
    "gold",
    "firebrick1",
    "skyblue"
  ),
  drop = FALSE
)

# Define fine colour palette
fine_colour <- scale_colour_manual(
  values =  c(
    "darkgreen",
    "chartreuse3",
    "darkolivegreen1",
    "gold",
    "orange",
    "firebrick1",
    "darkred",
    "gray80",
    "gray30",
    "grey55"
  ),
  drop = FALSE
)

The following plot shows point estimates and their 90% confidence intervals, coloured by the coarse effect classification.

ggplot(data = result, aes(x = rownames(result))) +
  geom_hline(yintercept = 0, linetype = "longdash", colour = "black") +
  geom_hline(yintercept = c(-1, 1), linetype = "dotdash") +
  geom_errorbar(aes(ymin = lcl, ymax = ucl, colour = effect_coarse),
                linewidth = 1.5, show.legend = TRUE) +
  geom_point(aes(y = mean), colour = "black", size = 3.5) +
  labs(x = "Observation", y = "Effect estimate", colour = "Effect (coarse)") +
  coarse_colour +
  theme_minimal()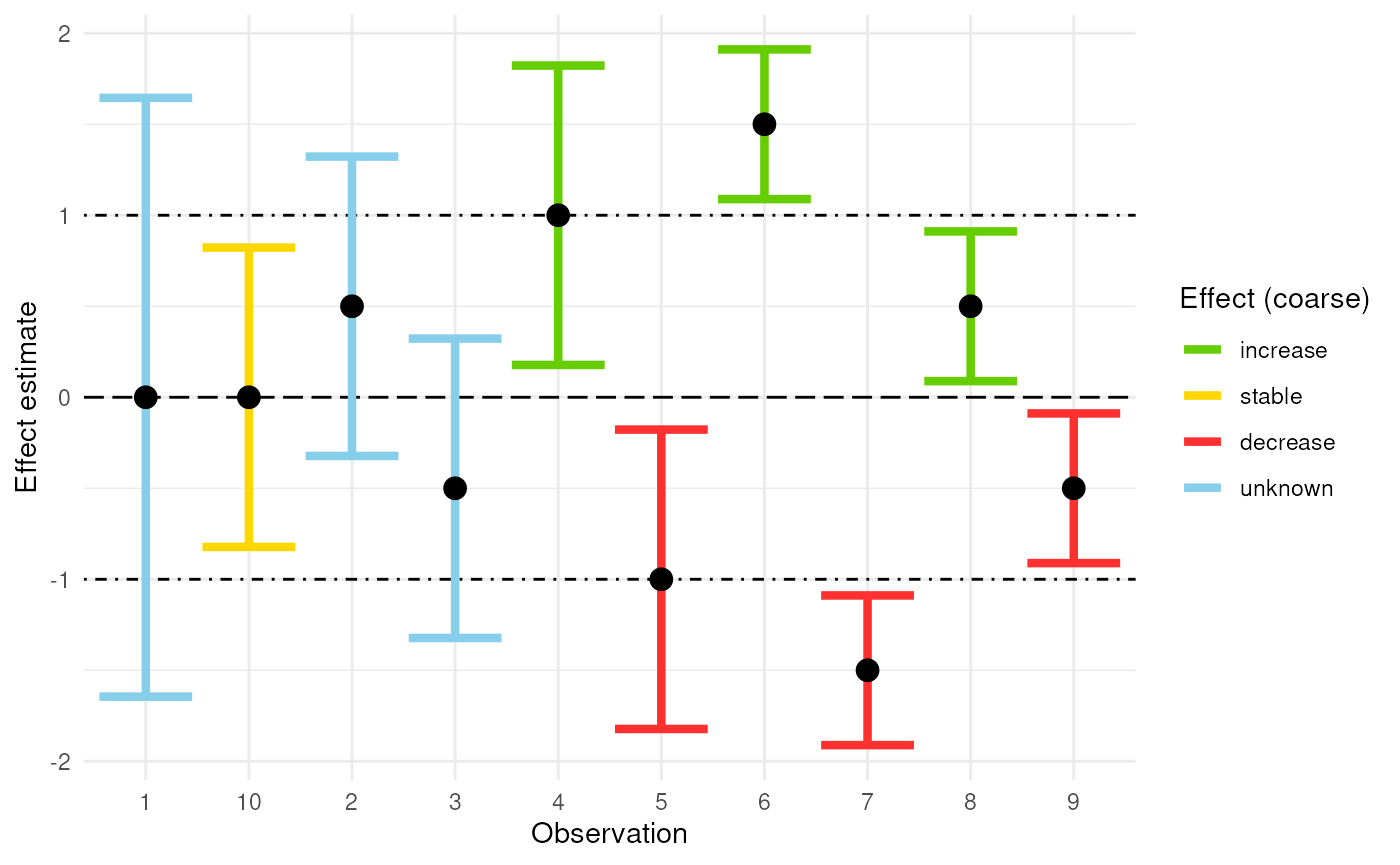

Visualising coarse effect classification.

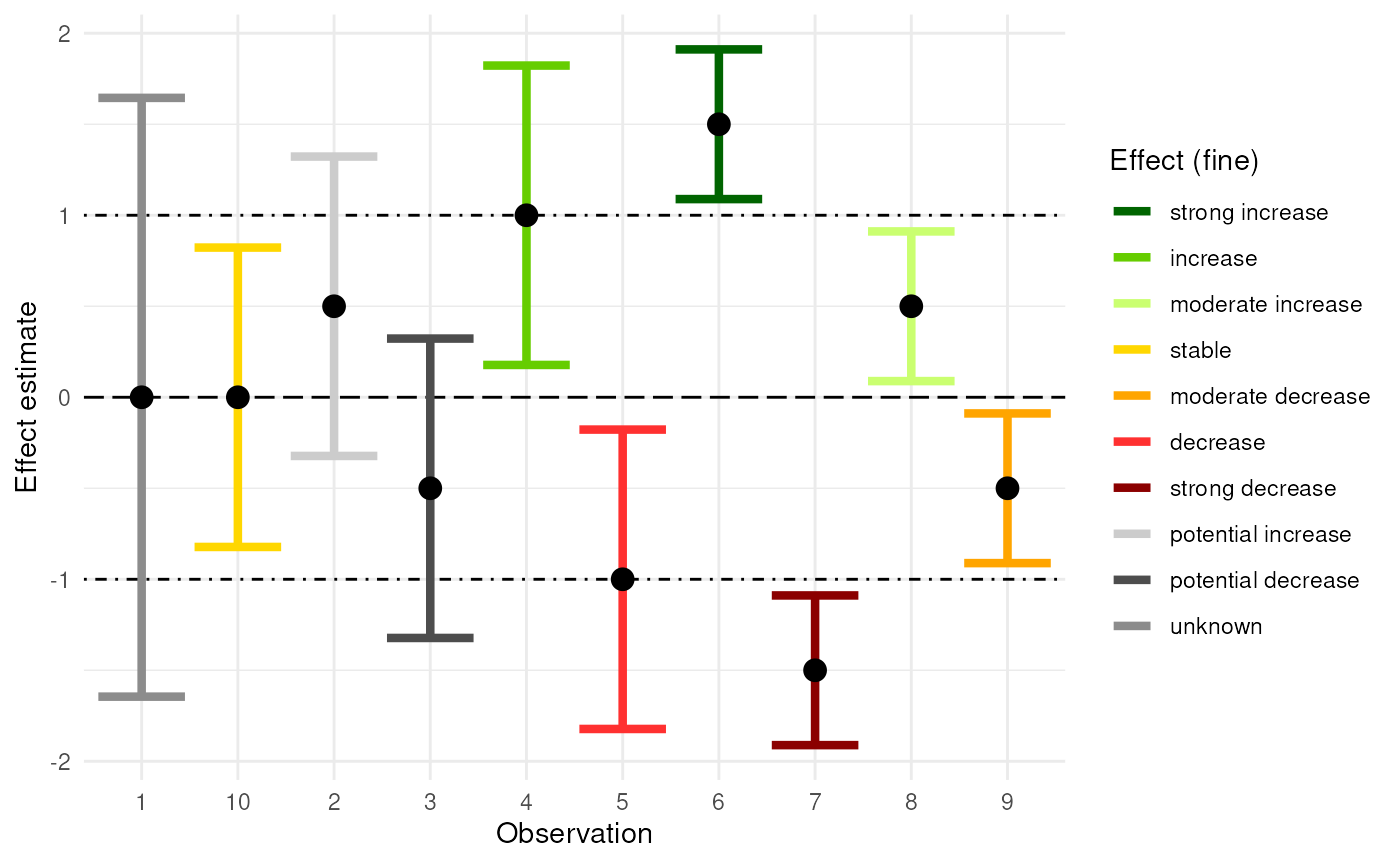
The plot below provides a more detailed view using the fine-grained classification.

ggplot(data = result, aes(x = rownames(result))) +
  geom_hline(yintercept = 0, linetype = "longdash", colour = "black") +
  geom_hline(yintercept = c(-1, 1), linetype = "dotdash") +
  geom_errorbar(aes(ymin = lcl, ymax = ucl, colour = effect),
                linewidth = 1.5, show.legend = TRUE) +
  geom_point(aes(y = mean), colour = "black", size = 3.5) +
  labs(x = "Observation", y = "Effect estimate", colour = "Effect (fine)") +
  fine_colour +
  theme_minimal()

Visualising fine effect classification.